Sifat-Sifat Logaritma(26 september 2018)

LOGARITMA

Pengertian Logaritma

Logaritma adalah operasi matematika yang merupakan kebalikan dari eksponen atau pemangkatan.

Rumus dasar logaritma:

bc= a ditulis sebagai blog a = c (b disebut basis)
Beberapa orang menuliskan blog a = c sebagai logba = c.
Logaritma
ac = b → ª log b = c
a = basis
b = bilangan yang dilogaritma
c = hasil logaritma

Sifat-sifat Logaritma

ª log a = 1
ª log 1 = 0
ª log aⁿ = n
ª log bⁿ = n • ª log b
ª log b • c = ª log b + ª log c
ª log b/c = ª log b – ª log c
ªˆⁿ log b m = m/n • ª log b
ª log b = 1 ÷ b log a
ª log b • b log c • c log d = ª log d
ª log b = c log b ÷ c log a

Sifat-sifat Logaritma

1. Sifat Logaritma dari perkalian

Suatu logaritma merupakan hasil penjumlahan dari dua logaritma lain yang nilai kedua numerus-nya merupakan faktor dari nilai nume

rus awal. Berikut modelnya:

^alog p.q = ^alog p + ^alog q

dengan syarat a > 0, 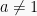$a \ne 1$ , p > 0, q > 0.

2. Perkalian Logaritma

Suatu logaritma a dapat dikalikan dengan logaritma b jika nilai numerus logaritma a sama dengan nilai bilangan pokok logaritma b. Hasil perkalian tersebut merupakan logaritma baru dengan nilai bilangan pokok sama dengan logaritma a, dan nilai numerus sama dengan logaritma b. Berikut model sifat logaritma nya:

^alog b x ^blog c = ^alog c

dengan syarat a > 0, 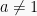$a \ne 1$ .

3. Sifat Logaritma dari pembagian

Suatu logaritma merupakan hasil pengurangan dari dua logaritma lain yang nilai kedua numerus-nya merupakan pecahan atau pembagian dari nilai numerus logaritma awal. Berikut modelnya:

^alog $\frac{p}{q}$ = ^alog p – ^alog q

dengan syarat a > 0, 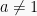$a \ne 1$ , p > 0, q > 0.

4. Sifat Logaritma berbanding terbalik

Suatu logaritma berbanding terbalik dengan logaritma lain yang memiliki nilai bilangan pokok dan numerus-nya saling bertukaran. Berikut modelnya:

^alog b = 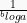$\frac{1}{^b log a}$

dengan syarat a > 0, 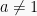$a \ne 1$ .

5. Logaritma berlawanan tanda

Suatu logaritma berlawanan tanda dengan logaritma yang memiliki numerus-nya merupakan pecahan terbalik dari nilai numerus logaritma awal. Berikut modelnya:

^alog $\frac{p}{q}$ = – ^alog $\frac{q}{p}$

dengan syarat a > 0, 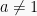$a \ne 1$ , p > 0, q > 0.

6. Sifat Logaritma dari perpangkatan

Suatu logaritma dengan nilai numerus-nya merupakan suatu eksponen (pangkat) dapat dijadikan logaritma baru dengan mengeluarkan pangkatnya menjadi bilangan pengali. Berikut modelnya :

^alog b^p = p. ^alog b

dengan syarat a > 0, 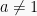$a \ne 1$ , b > 0

7. Perpangkatan Bilangan Pokok Logaritma

Suatu logaritma dengan nilai bilangan pokoknya merupakan suatu eksponen (pangkat) dapat dijadikan logaritma baru dengan mengeluarkan pangkatnya menjadi bilangan pembagi. Berikut modelnya:

$^{a^p} log b = \frac{1}{p} ^a log b$

dengan syarat a > 0, 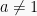$a \ne 1$ .

8. Bilangan pokok logaritma sebanding dengan perpangkatan numerus

Suatu logaritma dengan nilai numerus-nya merupakan suatu eksponen (pangkat) dari nilai bilangan pokoknya memiliki hasil yang sama dengan nilai pangkat numerus tersebut. Berikut model sifat logaritma nya:

^alog a^p = p

dengan syarat a > 0 dan 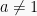$a \ne 1$ .

9. Perpangkatan logaritma

Suatu bilangan yang memiliki pangkat berbentuk logaritma, hasil pangkatnya adalah nilai numerus dari logaritma tersebut. Berikut modelnya:

$a^{^a log m} = m$

dengan syarat a > 0, 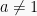$a \ne 1$ , m > 0.

10. Mengubah basis logaritma

Suatu logaritma dapat dipecah menjadi perbandingan dua logaritma sebagai berikut:

$^p log q = \frac{^a log p}{^a log q}$

dengan syarat a > 0, 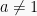$a \ne 1$ , p > 0, q > 0

hajril febrian

Sifat-Sifat Logaritma(26 september 2018)

0 Response to "Sifat-Sifat Logaritma(26 september 2018)"